
Significant Figures
 | Math Skills Review Significant Figures |
There are two kinds of numbers in the world:
Accuracy refers to how closely a measured value agrees with the correct value.
Precision refers to how closely individual measurements agree with each other.
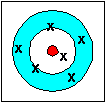 |  |  |
| accurate (the average is accurate) not precise | precise not accurate | accurate and precise |
Let's look at an example where significant figures is important: measuring volume in the laboratory. This can be done in many ways: using
A rule of thumb: read the volume to 1/10 or 0.1 of the smallest division. (This rule applies to any measurement.) This means that the error in reading (called the reading error) is 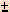 1/10 or 0.1 of the smallest division on the glassware. If you are less sure of yourself, you can read to 1/5 or 0.2 of the smallest division.
1/10 or 0.1 of the smallest division on the glassware. If you are less sure of yourself, you can read to 1/5 or 0.2 of the smallest division.
| Beaker | 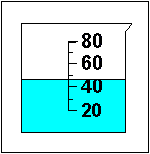 | The smallest division is 10 mL, so we can read the volume to 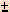 1/10 of 10 mL or 1/10 of 10 mL or 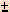 1 mL. The volume we read from the beaker has a reading error of 1 mL. The volume we read from the beaker has a reading error of 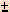 1 mL. 1 mL.The volume in this beaker is 47 So, How many significant figures does our volume of 47
|
| Graduated Cylinder |  Look in the textbook for a picture of a graduated cylinder. | First, note that the surface of the liquid is curved. This is called the meniscus. This phenomenon is caused by the fact that water molecules are more attracted to glass than to each other (adhesive forces are stronger than cohesive forces). When we read the volume, we read it at the BOTTOM of the meniscus. The smallest division of this graduated cylinder is 1 mL. Therefore, our reading error will be How many significant figures does our answer have? 3! The "3" and the "6" we know for sure and the "5" we had to estimate a little.
|
| Buret | 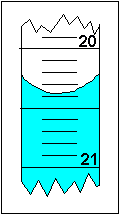 Look in the textbook for a picture of a buret. Note that the numbers get bigger as you go down the buret. This is different from the beaker or the graduated cylinder. This is because the liquid leaves the buret at the bottom. | The smallest division in this buret is 0.1 mL. Therefore, our reading error is 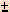 0.01 mL. A good volume reading is 20.38 0.01 mL. A good volume reading is 20.38 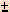 0.01 mL. An equally precise answer would be 20.39 mL or 20.37 mL. 0.01 mL. An equally precise answer would be 20.39 mL or 20.37 mL. How many significant figures does our answer have? 4! The "2", "0", and "3" we definitely know and the "8" we had to estimate.
|
Conclusion: The number of significant figures is directly linked to a measurement. If a person needed only a rough estimate of volume, the beaker volume is satisfactory (2 significant figures), otherwise one should use the graduated cylinder (3 significant figures) or better yet, the buret (4 significant figures).
So, does the concept of significant figures deal with precision or accuracy? Hopefully, you can see that it really deals with precision only. Consider measuring the length of a metal rod several times with a ruler. You will get essentially the same measurement over and over again with a small reading error equal to about 1/10 of the smallest division on the ruler. You have determined the length with high precision. However, you don't know if the ruler was accurate to begin with. Perhaps it was a plastic ruler left in the hot Texas sun and was stretched. You don't know the accuracy of your measuring device unless you calibrate it, i.e. compare it against a ruler you knew was accurate. Note: in the laboratory, a good analytical chemist always calibrates her volumetric glassware before using it by weighing a known volume of liquid dispensed from the glassware. By dividing the mass of the liquid by its density, she can determine the actual volume and hence the accuracy of the glassware.
Rules for Working with Significant Figures:
EXAMPLES:
| Example | Number of Significant Figures | Scientific Notation | ||
| 0.00682 | 3 | 6.82 x 10-3 | Leading zeros are not significant. | |
| 1.072 | 4 | 1.072 (x 100) | Imbedded zeros are always significant. | |
| 300 | 1 | 3 x 102 | Trailing zeros are significant only if the decimal point is specified. | |
| 300. | 3 | 3.00 x 102 | ||
| 300.0 | 4 | 3.000 x 102 |
EXAMPLES
| Addition |  | Even though your calculator gives you the answer 8.0372, you must round off to 8.04. Your answer must only contain 1 doubtful number. Note that the doubtful digits are underlined. |
| Subtraction |  | Subtraction is interesting when concerned with significant figures. Even though both numbers involved in the subtraction have 5 significant figures, the answer only has 3 significant figures when rounded correctly. Remember, the answer must only have 1 doubtful digit. |
| Multiplication |  | The answer must be rounded off to 2 significant figures, since 1.6 only has 2 significant figures. |
| Division |  | The answer must be rounded off to 3 significant figures, since 45.2 has only 3 significant figures. |
Notes on Rounding
| Question 1 | Give the correct number of significant figures for 4500, 4500., 0.0032, 0.04050 |
| Question 2 | Give the answer to the correct number of significant figures: 4503 + 34.90 + 550 = ? |
| Question 3 | Give the answer to the correct number of significant figures: 1.367 - 1.34 = ? |
| Question 4 | Give the answer to the correct number of significant figures: (1.3 x 103)(5.724 x 104) = ? |
| Question 5 | Give the answer to the correct number of significant figures: (6305)/(0.010) = ? |
Pick your next topic:
  Algebraic Manipulation Algebraic Manipulation |   Scientific Notation Scientific Notation |   Manipulation of Exponents Manipulation of Exponents |
  Dimensional Analysis Dimensional Analysis |   Logarithms Logarithms |   The Quadratic Equation The Quadratic Equation |