Algebraic Manipulation
| Math Skills Review Algebraic Manipulation |
The key to solving simple algebraic equations containing a single unknown (e.g. x + 6 = 10) is to realize that the equation is an equality. As long as you do the same mathematical operation (e.g. add a constant, subtract a constant, multiply by a constant, and divide by a constant) to both sides of the equation, the equality is still an equality. This includes squaring both sides of the equation or taking the square root of both sides of the equation.
Fundamental Laws:
| Example 1 | To solve for x, it is necessary to subtract 6 from both sides of the equation |  |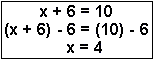
| Example 2 | To solve for x, you need to add 6 to both sides of the equation and then divide both sides by 2. |  |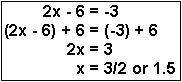
| Example 3 | To isolate x, you need to (1) multiply through by 6, (2) subtract 2 from both sides, and (3) divide both sides by 5. |  |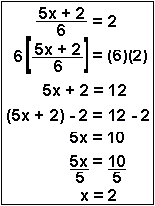
| Example 4 | To solve for x this time, you need to (1) multiply both sides of the equation by 4 and 3 to cancel out the denominator in line 2, |  |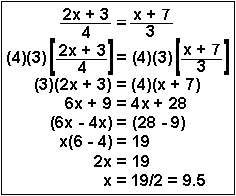
| Example 4 (alternative) | This process is called "cross-multiplying." This entails multiplying the numerator of one side of the equality by the denominator of the other side of the equality. When this is done, the very same line 3 results. The rest of the problem is done identically. |  |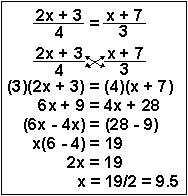
| Example 5 | This problem could be very complicated and become a quadratic equation. However, because it has a perfect square on both sides, if you simply take the square root of both sides of the equality, you are left in line 3 with a straightforward algebra problem as you solve for the positive root, which I did here.
In Chemistry, when we use this technique to solve equilibrium problems, only one of the roots is meaningful. Of course, the square root of 49 can be -7 as well as +7. You can then go ahead and solve for the second root, x = -0.8 = -4/5. |  |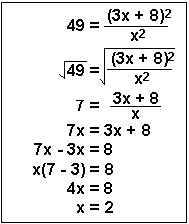
QUIZ: Solve for x.
| Question 1 | Question 2 | Question 3 | Question 4 |
 |  |  |  |
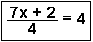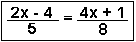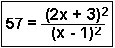  Dimensional Analysis | Significant Figures | Manipulation of Exponents |
| Scientific Notation | Logarithms | The Quadratic Equation |