Math Skills Review The Quadratic Equation

Many times in Chemistry, e.g. when solving equilibrium problems, a quadratic equation results. It has the general form:

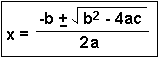
There are two roots (answers) to a quadratic equation, because of the 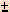in the equation. In most chemistry problems, only one answer will be meaningful and have physical significance. This means that one answer will make sense, the other answer won't. This will be obvious! Usually when the WRONG answer is plugged in, it will lead to a negative concentration or amount. Since nothing can exist as a negative concentration, the other answer must be the RIGHT one.

Let's work through a typical quadratic calculation that you might find in equilibrium problems.

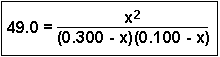
To expand the denominator, multiply the two terms together:

Then we have:

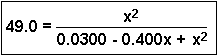
If we cross-multiply (See the review on Algebraic Manipulation), we get:

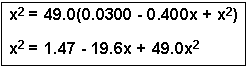
If we then subtract x² from both sides, we can rearrange the equation to get a quadratic equation:

Now, plug the numbers into the quadratic formula, where a = 48.0, b = -19.6 and c = 1.47:

Chemical Equilibrium Application: At this point, it may be difficult for you to see which root (answer) is useful and which one is not. Let me give you the original problem:

Consider the following equilibrium having an equilibrium constant = 49.0 at a certain temperature:

A(g) + B(g) C(g) and D(g)

If 0.300 mol of A and 0.100 mol of B are mixed in a 1.00 liter container and allowed to reach equilibrium, what concentrations of A and B will react and what concentrations of C and D will be formed?

In this particular problem, the initial concentrations of two reactants were 0.300 M and 0.100 M - these numbers appeared in the denominator of the original problem. The value of x represents the concentration of these reactants that were converted into products. If 0.309 M of one reactant was lost, that would leave behind (0.300 - 0.309) = -0.009 M of one reactant and (0.100 - 0.309) = -0.209 M of the other reactant. Since it is impossible to have a negative concentration remaining, the 0.309 number is extraneous (meaningless) and the other, x = 0.099 is the root we are interested in. Therefore, A and B both lost 0.099 M and the equilibrium concentrations of both C and D are 0.099 M.

Pick your next topic:

Algebraic Manipulation	Scientific Notation	Significant Figures
Dimensional Analysis	Manipulation of Exponents	Logarithms