 | Math Skills Review
Manipulation of Exponents |
Scientific calculations are frequently handled by expressing quantities in scientific notation. Such operations require simple manipulation of exponents, usually exponents of 10. When the same base is used (e.g. 10), the following rules apply:
When the operation involves multiplication, add the exponents algebrically.
- example: 103 x 104 = 10(3 + 4) = 107
- example: 105 x 102 x 10-3 = 10(5 + 2 + (-3)) = 104
When the operation involves division, subtract the divisor exponent from the numerator exponent.
- example: 105/103 = 10(5 - 3) = 102
- example: 107/1012 = 10(7 - 12) = 10-5
- example: 108/10-3 = 10(8 - (-3)) = 1011
- example: (106 x 104)/(103 x 102) = 10(6 + 4 - (3 + 2)) = 105
When the operation involves powers or roots, multiply the exponent by the power number or divide the exponent by the power number, respectively.
- example: (105)3 = 10(5 x 3) = 1015
- example: (10-7)4 = 10-(7 x 4) = 10-28
- example:
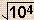 = (104)1/2 = 10(4 x 1/2) = 102
= (104)1/2 = 10(4 x 1/2) = 102
- example:
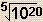 = (1020)1/5 = 10(20 x 1/5) = 104
= (1020)1/5 = 10(20 x 1/5) = 104
There are more complex examples in the section on Scientific Notation, as well as notes on using scientific calculators.
QUIZ: Give the correct answer.
| Question 1 | 103 x 10-4 = ? |
| Question 2 | 106/10-3 = ? |
| Question 3 | (102)4 = ? |
| Question 4 | 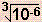 = ? = ? |
Answers: (1)10-1 (2) 109
(3) 108
(4) 10-2
Pick your next topic:


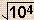 = (104)1/2 = 10(4 x 1/2) = 102
= (104)1/2 = 10(4 x 1/2) = 102
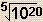 = (1020)1/5 = 10(20 x 1/5) = 104
= (1020)1/5 = 10(20 x 1/5) = 104
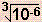 = ?
= ? 
 Algebraic Manipulation
Algebraic Manipulation
 Scientific Notation
Scientific Notation
 Significant Figures
Significant Figures
 Dimensional Analysis
Dimensional Analysis
 Logarithms
Logarithms
 The Quadratic Equation
The Quadratic Equation