
Dimensional Analysis
 | Math Skills Review Dimensional Analysis |
Dimensional Analysis (also called Factor-Label Method or the Unit Factor Method) is a problem-solving method that uses the fact that any number or expression can be multiplied by one without changing its value. It is a useful technique. The only danger is that you may end up thinking that chemistry is simply a math problem - which it definitely is not.
Unit factors may be made from any two terms that describe the same or equivalent "amounts" of what we are interested in. For example, we know that
We can make two unit factors from this information:
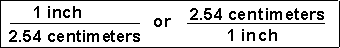
(1) How many centimeters are in 6.00 inches?
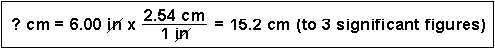
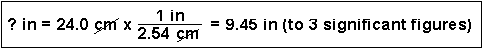
You can also string many unit factors together.
(3) How many seconds are in 2.0 years?
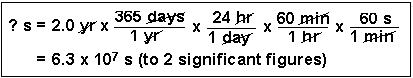
Scientists generally work in metric units. Common prefixes used are the following:
| Prefix | Abbreviation | Meaning | Example |
|---|---|---|---|
| mega- | M | 106 | 1 megameter (Mm) = 1 x 106 m |
| kilo- | k | 103 | 1 kilogram (kg) = 1 x 103 g |
| centi- | c | 10-2 | 1 centimeter (cm) = 1 x 10-2 m |
| milli- | m | 10-3 | 1 milligram (mg) = 1 x 10-3 g |
| micro- | 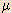 | 10-6 | 1 micrometer (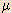 g) = 1 x 10-6 g) = 1 x 10-6 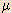 g g |
| nano- | n | 10-9 | 1 nanogram (ng) = 1 x 10-9 g |
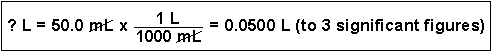
(5) What is the density of mercury (13.6 g/cm3) in units of kg/m3?
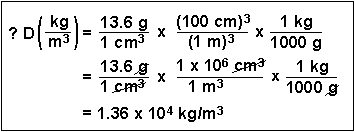
We also can use dimensional analysis for solving problems.
(6) How many atoms of hydrogen can be found in 45 g of ammonia, NH3?
We will need three unit factors to do this calculation, derived from the following information:

There are many, many more examples in your textbook!
QUIZ:
| Question 1 | How many millimeters are present in 20.0 inches? |
| Question 2 | The volume of a wooden block is 6.30 in3. This is equivalent to how many cubic centimeters? |
| Question 3 | A sample of calcium nitrate, Ca(NO3)2, with a formula weight of 164 g/mol, has 5.00 x 1027 atoms of oxygen. How many kilograms of Ca(NO3)2 are present? |
  Algebraic Manipulation Algebraic Manipulation |   Significant Figures Significant Figures |   Manipulation of Exponents Manipulation of Exponents |
  Scientific Notation Scientific Notation |   Logarithms Logarithms |   The Quadratic Equation The Quadratic Equation |