
Investigation #22:
 | Investigation #22:
|
Concepts of the Experiment
In this lab you will determine the ionization constant of a weak acid. "What is the ionization constant," you might ask? A good question and a good place to start. So let's first define and go over some concepts.
Strong Acid – An acid is strong if it completely or almost completely ionizes. An acid's strength has nothing to do with chemical properties such as corrosion however. Remember it only has to do with ionization. This may be expressed in the following generic formula:
HA « H3O+ + A-
Taking this generic equation and solving for the ionization constant, which we shall call the acid ionization constant, we get:
| Ka = | OR pKa = -log Ka = pH + log |
A strong acid will have a Ka value close to 1 and a negative pKa value while a weak acid will have a small Ka value <<1. For example, acetic acid has a Ka value of 1.8 x 10-5 and a pKa value of +4.76.
You will use these concepts to calculate the Ka of an unknown weak acid. To do this, you will measure out a certain mass of the unknown solid and dissolve it in 300 mL of boiled distilled H2O. You will then use the given density to determine the volume of the acid. This volume will be Vinitial.
Vinitial = (mass of beaker and solution – mass of beaker)/density.
Once you know the volume of the unknown acid, you will titrate it with
a standardized solution of NaOH. At the endpoint of the titration, the
moles of acid will equal the moles of base. In other words, the moles of
acid = mol/L NaOH x L NaOH titrated. Actually though, the previous
statement here is wrong. The endpoint in a titration does not actually
mean that the moles of acid = the moles of base. This is actually
the definition of equivalence point. The endpoint is actually a physical
phenomenon associated with a color change at some pH. For bromophenol
blue which we used in the last investigation this color change or endpoint
actually occurred at around pH = 4.6. The endpoint for phenolphthalein
is pH = 8.5. At pH of 7, the moles of acid will equal the moles of
base in a neutral solution. So in the past, we have made it easier
for you by assuming that these endpoints were actually very close to the
equivalence points. In this experiment, we will continue to assume
this as well. Are we justified in doing this? (answer at the
bottom of the page)
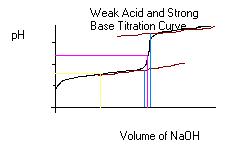
In this experiment, you added some known mass of unknown weak acid to a beaker and titrated with a standardized solution of NaOH. You should then be able to make a graph like the one above. From this graph, you can determine the equivalence point and the 1/2 equivalence point. At the graphically determined equivalence point, the moles of acid = moles of base. At the endpoint (color change) the moles of acid will almost equal the moles of base. Compare the two and see how close they are.
To make the graph you will plot your experimentally determined pH values on the ordinate (y-axis) and the total volume of NaOH (Vtitration- Vinitial) up to each of the pH readings on the abscicca (x-axis). Once you have your graph made you will use it to determine the equivalence point and the 1/2 equivalence point for the calculations.
When calculating the pH you will have to use some of the equations derived
below. The usefull ones are the equations at the 1/2 equivalence
point, the beginning point and the general Ka equation at any point.
It would help if you used a spreasheet program like excell. Don't
forget to at least show an example of your calculations.
Ka Equation Derivations
You will use a pH meter to determine the pH which will also tell you the hydronium ion concentration, H3O+. This will not be enough however to calculate Ka. We will also need [A-] and [HA]. So at this point we have three unknown, but only one equation. We need more equations to solve these unknowns so let's consider equations for charge balance and mass balance. These will be:
[H+] + [Na+] = [A-] + [OH-] charge balance
[A-] + [HA] = [HA]total mass balance
If you take the charge balance equation and rearrange solving for [A-] then take this and substitute into both the equations for Ka and mass balance you get:
| Ka = | 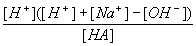 |
[HA] = [HA]total – [H+] – [Na+] + [OH-]
Now take this second equation and substitute it into the equation for Ka.
| Ka = | 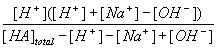 |
Examining this equation you will see a term for the concentration of [OH-]. If you are using an acidic solution however, this concentration must be very small and considered negligible. The equation can therefore be rewritten:
| Ka = | 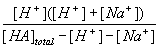 |
Examining this equation, your unknowns are [HA]total and [Na+]. You can find these using the same principles we have used throughout titration reactions.
| [HA]total = | 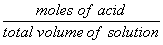 |
= | 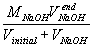 |
HA + NaOH ® Na+ + A- + H2O in an aqueous solution
| [Na+] = | 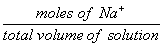 |
= | 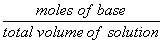 |
= | 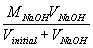 |
Substituting these into are ongoing large equation gives (general Ka equation):
| Ka = | 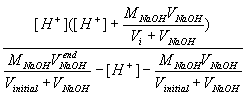 |
This big mess can thankfully be simplified. At the beginning of the experiment, the VNaOH is equal to 0 since none of the NaOH has been added. Also, if you compare the concentrations of [HA]total and [H+], the concentration of [H+] is negligible in comparison. This big equation therefore simplifies to:
| Ka = | 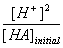 |
The big messy equation can also be simplified at the half-neutralization
point, ![]() .
This simplifies to:
.
This simplifies to:
Ka = [H+] or pKa = pH
Answers
If you look at the volume of titrant which would accompany the difference between the endpoint and the equivalence point, this will usually be very small. This is especially true when the overall volume of titrant is large. The small volume difference becomes more negligible with larger volumes of titrant.