Welcome to Lindahl Lab
Biophysical and Bioinorganic Chemistry
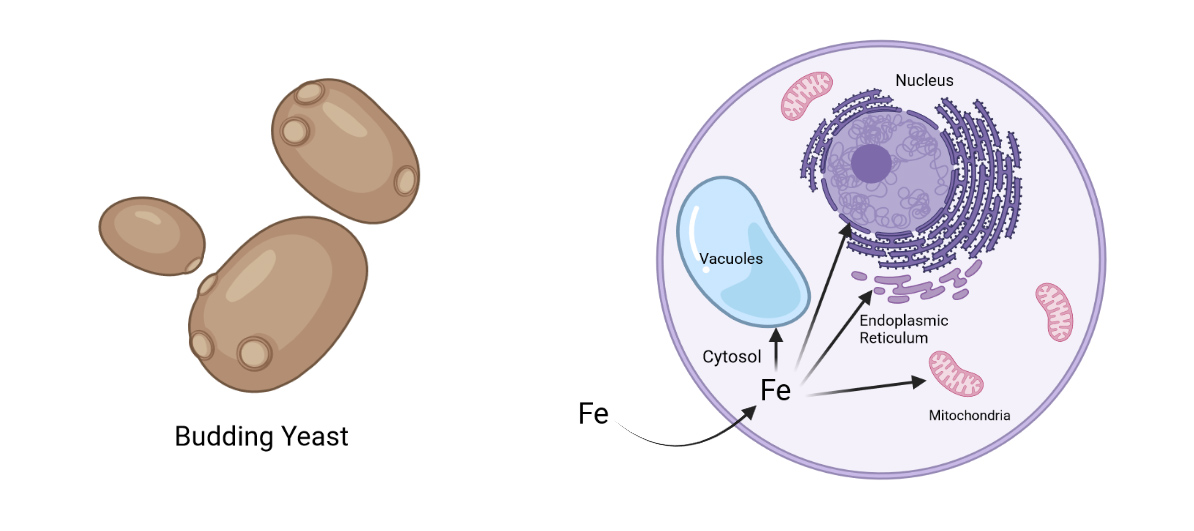
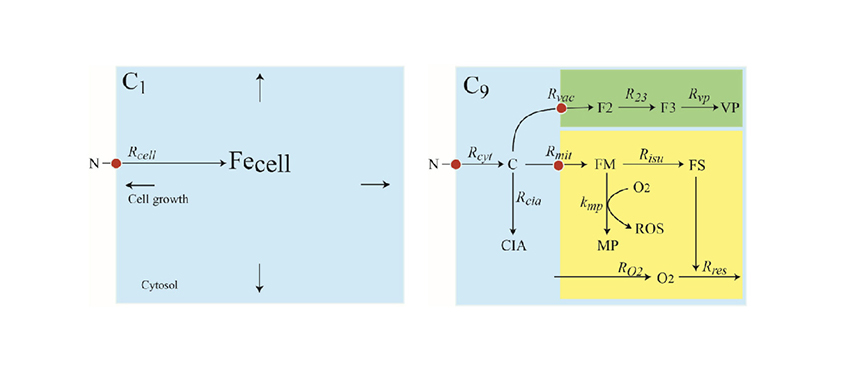
Iron Metabolism in Cells
Mechanistic Modeling of Biological Processes
EPR and Mössbauer Spectroscopy
Systems Biology
Research Areas
Metalomics of a Yeast Cell
We isolate organelles from yeast cell to understand metal trafficking at a granular level. Mitochondria are of particular interest because they are the 'hub' of iron metabolism.
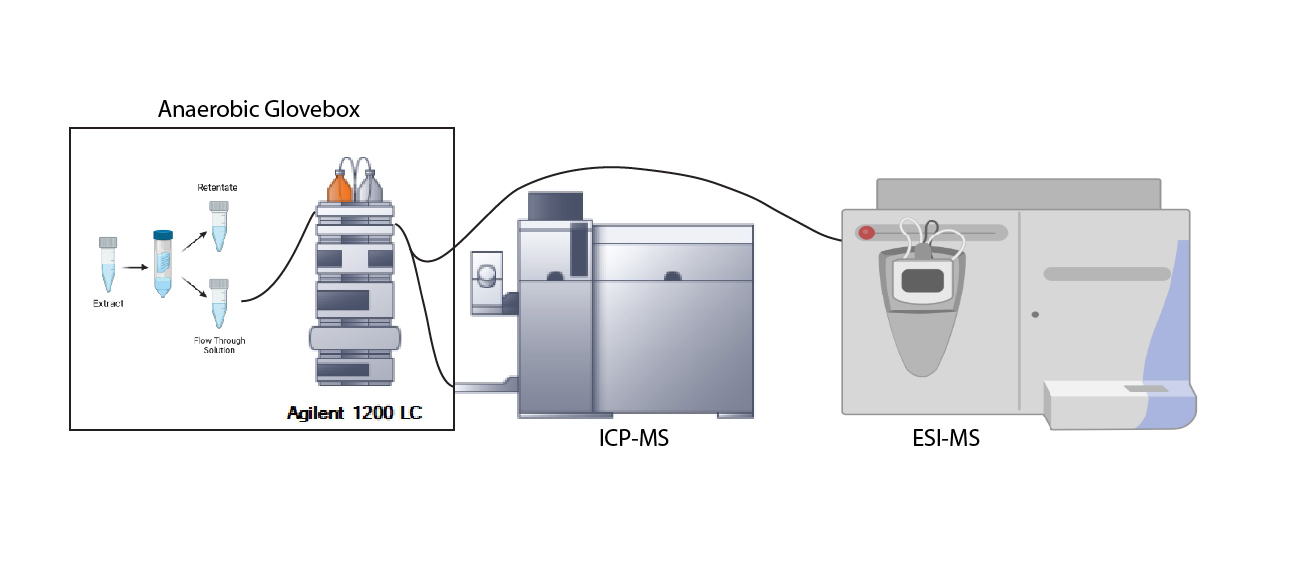
Labile Metal Pools
LMPs consist of small metal complexes with nonproteinaceous ligands. We are using liquid-chromatography interfaced with inductively-coupled plasma mass spectrometry (LC-ICP-MS) to detect, identify, and characterize these pools.